출처: Baroody, A. J., Feil, Y., & Johnson, A. R. (2007). Research commentary: An alternative reconceptualization of procedural and conceptual knowledge. Journal for research in mathematics education, 38(2), 115-131.
https://www.jstor.org/stable/30034952
2005년 11월 이 저널의 "Research Commentary"에서 ("Reconceptualizing Procedural Knowledge"), Jon Star는 수학 교육자들에게 절차적 지식(procedural knowledge)과 개념적 지식(conceptual knowledge)의 구성 요소를 명확하고 신중하게 고려하도록 도전하며 가치 있는 학문적 기여를 하였습니다. 그의 주장의 핵심은 de Jong과 Ferguson-Hessler (1996)와 마찬가지로, 이러한 용어들이 지식의 범주나 유형(예: 절차적 지식)과 지식의 속성이나 특성(예: 연결 정도)을 혼동한다는 것입니다. 이러한 특성은 어떤 유형의 지식에도 적용될 수 있습니다.
STAR의 절차적 지식과 개념적 지식의 재개념화 제안
STAR'S PROPOSAL FOR RECONCEPTUALIZING PROCEDURAL AND CONCEPTUAL KNOWLEDGE
Star(2005)는 절차적 지식이든 개념적 지식이든 각각 얕은(small) 품질 또는 깊은(deep) 품질을 가질 수 있다고 주장합니다. 그는 이 전제를 다음과 같이 네 가지 명확한 지식 범주로 제안합니다(J. Star, 개인적 의사소통, 2005년 12월 23일):
"풍부한 연결성이 없는 지식은 수학 교육자들 사이에서 일반적으로 절차적 지식으로 여겨집니다.... ‘개념적’이라는 형용사는 종종 풍부한 연결을 의미하는데 사용됩니다. 하지만 지식의 이러한 사용은 본질적으로 잃어버린 것과 다름없습니다. 흔히 절차적 지식은 절차에 대한 지식이라고 이해되지만, 이는 실제로 연결성을 뜻합니다."
Star는 2005년 논평에서, 절차적 지식을 얕고 드문드문 연결된 기계적인 지식과 동일시하고, 개념적 지식을 깊고 풍부하게 연결된 의미 있는 지식과 동일시하는 것은 "깊은 절차적 지식" 또는 "얕은 개념적 지식"에 속하는 지식을 고려하거나 이름을 붙이기 어렵게 만든다고 결론지었습니다(p. 408). 이러한 혼란은 또한 "유연한 절차 사용을 뒷받침하는 지식"을 논의하는 것도 어렵게 만듭니다(J. Star, 개인적 의사소통, 2005년 12월 23일). Star(2005)는 유연성이 "깊은 절차적 지식의 핵심 지표"이지만, 수학 교육 연구에서는 자주 간과되며 "개념적 및 절차적 지식의 일반적인 정의에서조차 고려되지 않는다"고 지적했습니다(p. 409).
de Jong과 Ferguson-Hessler(1996)와 마찬가지로, Star(2005)는 지식의 유형과 품질을 독립된 차원으로 취급해야 한다고 주장했습니다. 이를 명확히 하기 위해 그는 개념적 지식을 "개념이나 원칙에 대한 지식"으로 정의했으며, 이는 관계나 연결을 포함하지만 반드시 풍부한 것은 아니라고 했습니다. 절차적 지식은 "절차에 대한 지식"으로 정의되었으며, 깊은 절차적 지식은 "이해, 유연성, 비판적 판단"을 포함하며 개념적 지식과는 다르지만 관련이 있을 수 있다고 설명했습니다(p. 408).
STAR의 제안에 대한 평가
AN EVALUATION OF STAR'S PROPOSAL
수학교육 연구자들의 견해
Mathematics Education Researchers' Views
만약 Hiebert와 Lefevre(1986)의 개념적 지식의 초기 정의와 절차적 지식에 대한 그들의 설명이 독립적으로 고려된다면, Star(2005)는 그들이 지식 유형과 품질을 혼동했다고 말하는 것이 맞습니다. Hiebert와 Lefevre는 전자를 "관계가 풍부한 지식"으로 정의했으며, "고립된 정보의 단편으로 존재할 수 없다"고 했습니다(pp. 3-4; Gray & Tall, 1994; Hiebert & Wearne, 1986 참조). 많은 종류의 관계로 가득 찬 개념적 지식과는 달리, Hiebert와 Lefevre는 절차적 지식을 주로 순차적 관계를 포함하는 것으로 묘사했습니다. 그 후 일부 수학교육자들, 특히 이 논평의 첫 번째 저자는 그들의 주장을 지나치게 단순화하고, "암기된 지식을 계산 기술 또는 절차적 지식과 무심코 동일시"한 적이 있었습니다(Baroody, 2003, p. 4).
수학교육 연구자들(MERs)은 절차적 지식을 일반적으로 지식의 유형으로 정의하는데, 이는 순차적이거나 "과제를 수행하는 단계별 처방"(Hiebert & Lefevre, 1986, p. 6; Haapasalo, 2003 참조)으로, 덧셈과 같은 과정을 구현하는 알고리즘(Davis, 1983; Gray & Tall, 1994; Hiebert & Lefevre; Nesher, 1986)으로, "방법을 아는 지식"으로(Skemp, 1987), 또는 '방법을 아는 것'과 '이유를 아는 것'을 결합한 지식(Baroody, 1998, 2003; Mason Spence, 1999)으로 정의합니다. 더 중요한 것은, 대부분의 MERs는 절차적 지식과 개념적 지식을 모두 드문 연결성에서 풍부한 연결성으로 이어지는 연속선으로 보는 방식으로 지식의 유형과 품질을 구분하려 시도한다는 점입니다(Baroody, 2003; Hiebert & Carpenter, 1992; Hiebert & Wearne, 1986; Moursund, 2002; Resnick & Ford, 1981). 예를 들어, Hiebert와 Lefevre는 절차적 지식을 관계가 없는 지식으로 한정하지 않으며, 절차가 종종 다른 절차에 포함되어 있다는 사실을 지적합니다(J. Hiebert, 개인적 의사소통, 2006년 8월 24일). 따라서 MERs는 일반적으로 약하게 연결된 지식을 절차적 지식과 동일시하지 않습니다(개인적 의사소통: T. Carpenter, 2006년 7월 11일; K. Fuson, 2006년 7월 24일; J. Hiebert, 2006년 7월 12일; L. Verschaffel, 2006년 7월 17일). "절차적 지식에는 본질적으로 '드문 연결...'이라는 속성이 없으며, 절차적 지식이 아닌 드문 연결의 개념적 지식이 많다"(D. Clements, 개인적 의사소통, 2006년 7월 12일).

MERs는 깊은 절차적 지식과 얕은 개념적 지식을 정의하고 연구하려고 시도해 왔습니다. 이들은 오랫동안 연결되지 않은, 무의미하고, 맥락에 얽매이며, 기계적인 절차(이를 '약한 체계'라고 부를 수 있음)를 잘 연결되고, 맥락화된, 통합되고, 의미 있으며, 전략적인 절차적 지식(이를 '강한 체계'라고 부를 수 있음)과 대조해 왔습니다(표 1의 A 행 참조). 비슷하게, 잘 연결된 개념적 지식은 드문 연결의 개념적 지식과 대조됩니다(표 1의 B 행 참조). 예를 들어, 광범위한 일반화, 높은 수준의 내부 논리적 일관성, 원칙 기반의 이해, 선험적 추론의 원칙적 기초(즉, 논리적으로 도출된 예측)를 포함하는 강한 체계는 깊은 개념적 지식을 뒷받침한다고 제안되었습니다. 반면, 국소적인 일반화, 낮은 수준의 내부 논리적 일관성, 선례에 의존한 이해, 선험적 추론의 논리적 기초가 없는 약한 체계는 얕은 개념적 지식을 뒷받침한다고 가정되며, 어린 아이들의 개념이 성인이나 더 나이 든 아이들보다 덜 깊고 덜 정교한 이유를 설명할 수 있습니다(예: 덜 일반적이고, 덜 논리적이며, 덜 상호 연결되거나 덜 유연함)(표 1의 B 행 참조).
MERs는 또한 절차적 지식과 개념적 지식 모두에 적용되는 개념들을 제시했으며, 각각의 얕고 깊은 형태가 많은 특성을 공유한다고 제안했습니다(표 1의 C 행 참조). 예를 들어, 얕은 개념적 및 절차적 지식은 기존에 익숙한 작업에 효과적으로 적용할 수 있는 지식인 '일상적 전문성'으로 설명되고, 깊은 개념적 및 절차적 지식은 새로운 작업뿐만 아니라 익숙한 작업에도 창의적이고 유연하며 적절하게 적용할 수 있는 '적응적 전문성'으로 묘사됩니다.
예를 들어, 어린 아이들이 이차원 도형의 다양한 종류(예: 삼각형, 정사각형, 직사각형, 원)의 이름을 기계적으로 암기한다고 생각해 봅시다. Hiebert와 Lefevre(1986)를 좁게 해석하는 MERs는 이러한 연결되지 않은 지식을 절차적 지식으로 정의할 수 있습니다(수학적 표현의 표면적 특징에 대한 지식). 하지만 대부분의 MERs는 이를 연결되지 않거나 드문 연결의 개념으로 정의할 것입니다. 이는 van Hiele(1986)의 1단계(시각화)에 해당합니다. 약한 체계와 일치하게, 1단계 사고자는 선례를 사용하여 기계적으로 도형을 인식하고, 분류하고, 이름을 붙입니다(Clements, Swaminathan, Hannibal, & Sarama, 1999). 예를 들어, 'D는 정사각형이고 직사각형이 아닌 이유는 정사각형처럼 보이고 직사각형처럼 보이지 않기 때문'이라고 할 수 있습니다. 반면에 2단계 이해(비공식적 추론)는 개념 속성들이 어떻게 상호 관련되는지를 이해하여 정사각형이 직사각형의 특별한 종류라는 사실을 인식하는 데 기반합니다.
요약하자면, 일부 MERs는 드문 연결 지식을 절차적 지식으로, 풍부하게 연결된 지식을 개념적 지식으로 독점적으로 동일시할 수 있지만, 아마도 대부분은 그렇지 않습니다. 그럼에도 불구하고, Star(2005)의 지적처럼, 수학 교육자들이 절차적 지식과 개념적 지식을 명확하고 일관된 방식으로 정의하지 못하고 있다는 점은 유효합니다.
개념적 지식과 절차적 지식의 정의
Definitions of Conceptual and Procedural Knowledge
Star(2005)는 지식의 유형과 품질을 명확하게 구분하지 않았습니다. 그는 깊은 절차적 지식의 예로 vanLehn(1990)이 제시한 "절차의 목적론적 이해"를 인용했는데, 이는 절차의 설계나 사용에 대한 정당성을 이해하는 것을 말합니다. 그러나 절차에 대한 지식은 표면적일 수도 있고(예: 절차의 단계를 순서대로 암기), 깊을 수도 있습니다(예: 단계들이 목표를 달성하기 위해 어떻게 상호 관련되는지에 대한 명확한 설명을 할 수 있음). 전자는 개념적 지식이 필수적이지 않지만, 절차의 깊은 이해가 그 절차의 논리적 근거(예: 각 단계의 개념적 기초)를 이해하지 않고 존재할 수 있는지에 대해서는 명확하지 않습니다. 수학적 절차는 진공 상태에서 만들어지지 않으며, 문제를 해결하기 위해 만들어지고 수학적 원칙과 논리에 따라 단계가 구성됩니다. 마찬가지로, 깊은 개념적 지식은 수학적 아이디어를 적용하고 확장하는 도구를 아는 것에 의존합니다(Kilpatrick, Swafford, & Findell, 2001). 따라서 지식의 품질과 유형을 이론적으로 구분하려는 시도는 타당하지만, 심리학적으로는 깊은 절차적 지식과 개념적 지식을 분리할 수 없습니다.
Star(2005)는 개념을 심리학자들이 정의한 것처럼, 등가성 집합equivalence class으로 정의할 것을 제안했습니다(Piaget, 1965; 하지만 Davis, 1983은 다르게 봄). 예를 들어, 개의 개념을 학습하는 것은 그 집합의 모든 구성원이 공통으로 가지는 속성을 유추하는 것을 포함합니다(Mix, Sandhofer, & Baroody, 2005). 그러나 Star가 인정하듯이, 이러한 정의는 반드시 풍부한 연결성을 의미하지 않더라도, 연결된 지식을 함축합니다. 그의 개념적 지식에 대한 설명은 Hiebert와 Lefevre(1986)가 처음 제시한 것과는 다르지만, 개념적 지식을 연결성의 연속선으로 보는 MERs의 관점과는 다르지 않습니다. Hiebert 자신도 이러한 견해를 가지고 있었습니다(예: Baroody, 1992; Hiebert & Carpenter, 1992; Lunkenbein, 1985; Resnick & Ford, 1981). Hiebert와 Lefevre는 개념적 지식이 동화와 통합을 통해 추가적인 연결이 이루어질수록 성장한다고 명확히 암시했습니다. Hiebert와 Wearne(1986)은 자리 값(place value)에 대한 개념적 네트워크가 "관련된 지식의 단편들이 이전의 아이디어와 연결될 때" 성장한다고 언급하며 이를 설명했습니다(p. 200). 지식의 품질이 연결의 수(그리고 그 질)에 의해 정의되기 때문에, 지식의 품질과 유형을 완전히 구분하려면 연결을 암시하는 개념적 지식을 정의해야 합니다.
유연성(Flexibility)과 깊은 절차적 지식의 지표
Flexibility as an Indicator of Deep Procedural Knowledge
Star(2005)의 예시는 유연성을 전략적으로 가장 효율적인 절차를 선택하는 능력과 동일시하는 것으로 보입니다. 그러나 유연성은 또한 새로운 과제 요구에 맞게 절차를 창의적으로 수정하는 능력을 의미할 수도 있습니다. 심리학자들(예: Ilg & Ames, 1951; Siegler & Shrager, 1984; Svenson 등)과 Wertheimer(1945/1959)와 같은 이론가들의 영향을 받아 MERs(수학교육 연구자들)는 오랫동안 절차적 유연성과 그 발달적 전제 조건에 대해 관심을 가져왔습니다(리뷰: Clements, 1983; Fuson, 1992; Ginsburg, Klein, & Starkey, 1998; Hiebert et al., 1997; Kilpatrick et al., 2001; Resnick 등). Richards와 Briars(1982), Steffe와 von Glasersfeld(1983), 그리고 Gray와 Tall(1994)는 "유연성은 문헌에서 중요한 특징이다"라고 관찰했습니다(p. 25). 이들의 관찰은 이후 Ambrose, Baek, & Carpenter(2003), Baroody(1995), Blite, Klein, & Beishuizen(2000) 등의 연구에서도 반복되었습니다. Carpenter 등(2003), Heirdsfield & Cooper(2002), Peled & Segalis(2005), Torbeyns, Verschaffel, & Ghesquiere(2005) 등도 유연성, 전략 선택, 여러 전략, 전이 등의 개념을 다루었습니다(Dowker, 2003).
MERs는 "유연한 접근법은 비정형 문제를 해결하는 데 필수적"이라는 데에 널리 동의하고 있습니다(Kilpatrick et al., 2001). 절차적 유창성은 유연하고 효율적인 절차의 사용을 포함해야 하며, 이러한 중요한 구성 요소는 개념적 이해와 상호작용하면서 서로 이득을 주고받는다는 점도 강조되었습니다(Davis, 1983; Gray & Tall, 1994; Ma, 1999). MERs는 개념적 지식과 절차적 지식의 통합을 다양한 방식으로 설명해왔습니다. 예를 들어, 적응적 전문성(adaptive expertise)의 개념은 깊은 절차적 지식과 유연성을 통합하는 개념입니다(Hatano, 2003). Hatano(2003)는 적응적 전문성의 산출물에 대해 추측하며, "유연성과 적응력은 개념적 지식을 기반으로 하여 대안들 사이에서 선택 기준을 제공하는 데 중요한 역할을 한다"고 언급했습니다(p. xi).
덧붙여서, MERs는 또한 믿음(beliefs)과 같은 다른 요인들이 유연한 문제 해결에서 어떤 역할을 하는지에 대해서도 고려했습니다(예: McLeod, 1992; Schoenfeld, 1985, 1992). 의미 있고 깊은 절차적 지식의 지표로서 MERs는 절차의 유연한 적용, 즉 적응적 전문성을 오랫동안 평가의 중요한 요소로 간주해왔습니다(Baroody, 2003; Carpenter, 1986; Haapasalo, 2003; Hatano, 1988, 2003; Kilpatrick et al., 2001 참조).
그러나 Star는(개인적 의사소통, 2005년 12월 23일) 기존의 깊은 절차적 지식 정의가 충분하지 않다고 생각합니다. 그는 다음과 같이 주장합니다:
"절차의 유연한 사용이 개념적 지식과 절차적 지식의 통합(예: 적응적 전문성)의 결과라고 말하는 것은 절차적 지식의 핵심 문제를 우회하는 것입니다. 절차적 지식(또는 기술)은 그 자체로 가치가 있으며, 단지 개념적 지식과의 연결이나 통합 때문에 가치 있는 것이 아닙니다."
Star(2005)의 절차적 및 개념적 지식 모델
Star(2005)는 절차적 지식과 개념적 지식이 직교(orthogonal) 관계에 있다는 모델을 제안합니다. 이 모델에 따르면, 깊고 유연한 절차적 지식은 개념적 지식이 있거나 없더라도 달성될 수 있습니다. 즉, 이는 적응적 전문성(adaptive expertise)을 통해서 이루어질 수 있으며(그림 1의 A 셀 및 어느 정도 B1, B2 셀), 또는 개념적 지식과의 연결 없이 이루어질 수 있습니다(즉, 주로 비개념적 지식과의 연결을 통해 이루어짐, 그림 1의 B3, B4 셀에 해당).
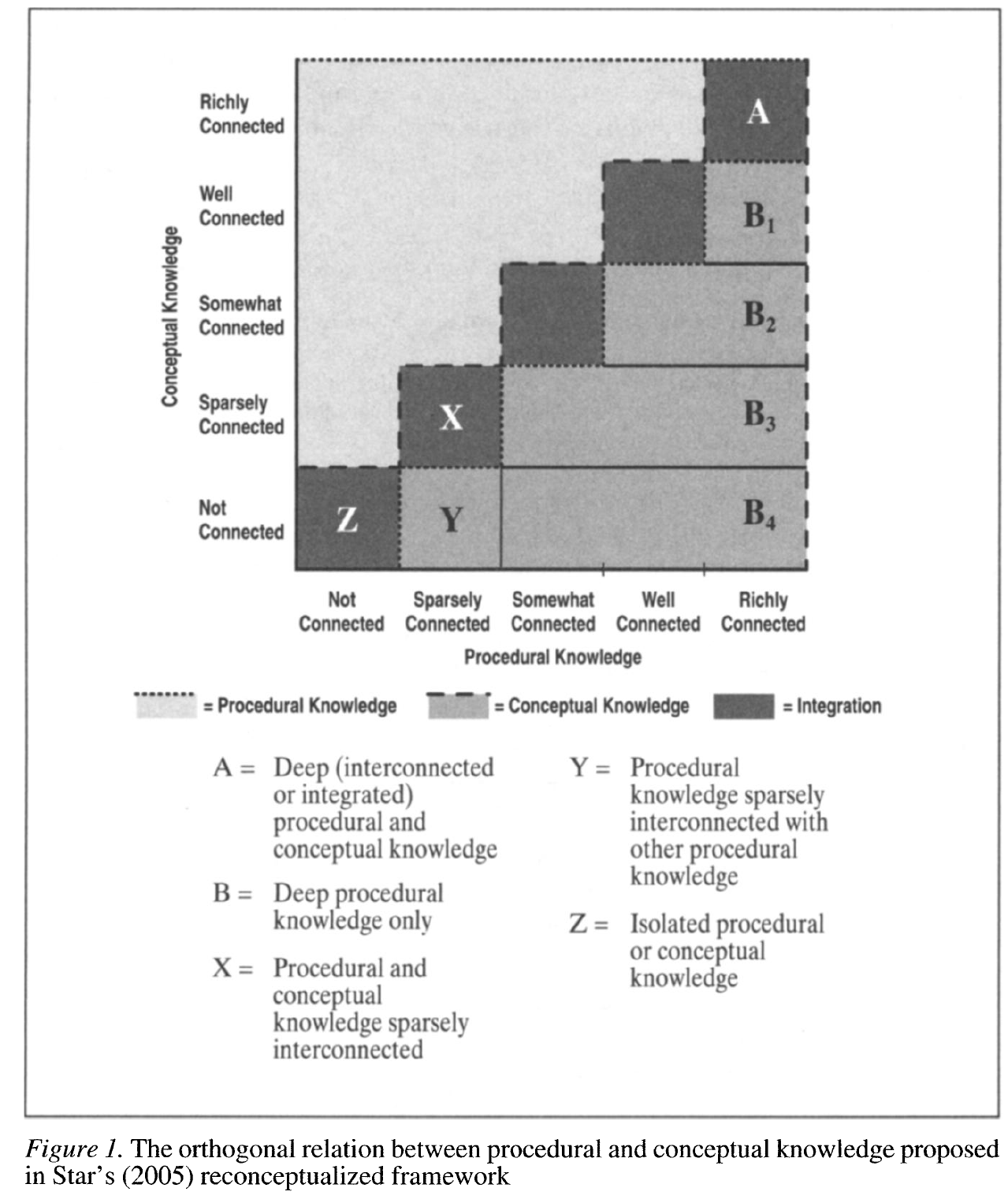
기존의 증거는 절차적 이해와 마찬가지로, 상당한 절차적 유연성과 비판적 판단력이 절차적 지식과 개념적 지식의 통합을 필요로 한다는 통념을 뒷받침하는 것으로 보입니다. 이는 단순히 비개념적 지식과의 다수의 연결만으로는 이루어질 수 없습니다(Carpenter, 1986; Carpenter, Levi, Franke, & Zeringue, 2005; Davis, 1983; Hatano, 2003). 예를 들어, Wertheimer(1945/1959)는 기계적으로 학습한 알고리즘을 다소 새로운 문제에 유연하게 적용하지 못한 아이들에 대한 관찰을 통해, 절차적 지식과 개념적 지식을 연결해야 할 필요성을 강조했습니다(Baroody, 2003; Resnick & Ford, 1981; Schoenfeld, 1986; Steffe, 1992).
Felicia(Baroody, 1984)의 사례를 생각해봅시다. 이 5세 아이는 주로 작은 숫자의 덧셈 문제를 더 큰 숫자에서 시작해 모두 세는 방법(CAL)을 사용해 풀었습니다(예: 3 + 5: "1, 2, 3, 4, 5; 6 [1 더하기], 7 [2 더하기], 8 [3 더하기]"). 더 어려운 문제를 받았을 때, Felicia는 더 효율적인 큰 숫자에서 세기(COL) 전략으로 유연하게 전환했습니다(예: 3 + 25: "25; 26 [+1], 27 [+2], 28 [+3]"). 하지만 그녀의 이해와 유연성은 제한적이었습니다. 다시 기본 문제를 받았을 때, Felicia는 다시 덜 발전된 CAL 절차로 돌아갔으며, COL 전략이 틀렸다고 주장했습니다. 이는 비교적 추상적이고 고급 전략을 아직 개발하지 않은 아이들에게서 나타나는 반응과 유사했습니다(Baroody, Tiilikainen, & Tai, 2006). 이러한 결과는 몇 개월 간격으로 두 번 재현되었습니다. 따라서 인지적 노력을 줄이기 위한 시도와 같은 비개념적 요인이 새로운 절차를 유연하게 발명하고 선택하며 사용하는 데 기여할 수 있지만, 이러한 요인이 제한적인 역할만 할 가능성이 큽니다(Carpenter, 1986).
개념적 이해와 절차적 유연성의 관계에 대한 의문
개념적 이해와의 통합이 절차적 유연성의 유일한 원천이라는 통념을 의심해볼 필요가 있습니다. 예를 들어, Hatano(2003)는 알고리즘의 각 단계에 대한 개념적 지식이 절차적 적응성에 필수적이라고 주장하면서 통합된 지식의 중요성을 과장했을 수 있습니다. 그러나 수학 교육자들이 이론이나 연구에서 유연성이나 그 기초를 간과했다고 결론짓는 것은 부정확합니다.
절차적 지식과 개념적 지식의 대안적 재개념화
AN ALTERNATIVE RECONCEPTUALIZATION OF PROCEDURAL AND CONCEPTUAL KNOWLEDGE
절차적 지식, 개념적 지식, 그리고 유연성 사이의 관계에 대한 연구를 촉진하기 위해, 우리는 Star의 재개념화 시도에 대한 대안을 제안합니다(그림 2 참조). Star의 제안에 따라 연결성의 정도와 독립적으로 지식 유형을 정의해야 한다는 권고에 동의하며, 우리는 de Jong과 Ferguson-Hessler(1996)의 정의를 수정하여 제안합니다. 즉, 절차적 지식을 과제를 완수하기 위한 규칙, 전략, 알고리즘을 포함한 정신적 "행동 또는 조작"(p. 107)으로 정의하고, 개념적 지식을 "사실, 일반화, 원칙에 대한 지식"(p. 107)으로 정의합니다. Star의 모델과 마찬가지로, de Jong과 Ferguson-Hessler의 모델과 달리 우리는 단순성을 위해 두 가지 지식 유형만 구분합니다. de Jong과 Ferguson-Hessler가 상황적 지식(문제 상황 또는 문제를 표현하거나 추가 정보를 찾기 위한 근거를 제공할 수 있는 특징에 대한 지식)이라 부르는 것을 우리는 절차적 또는 개념적 지식에 대한 완전하고 정확한 이해에 필요한 다른 지식으로 간주합니다(그림 2의 수평축). 그들이 전략적 지식이라 부르는 것은 절차적 지식으로 볼 수 있으며, 단순히 암기된 경우에는 절차적 지식으로, 의미 있는 문제 해결에 대한 절차적 및 개념적 지식의 결합으로 볼 수 있습니다.
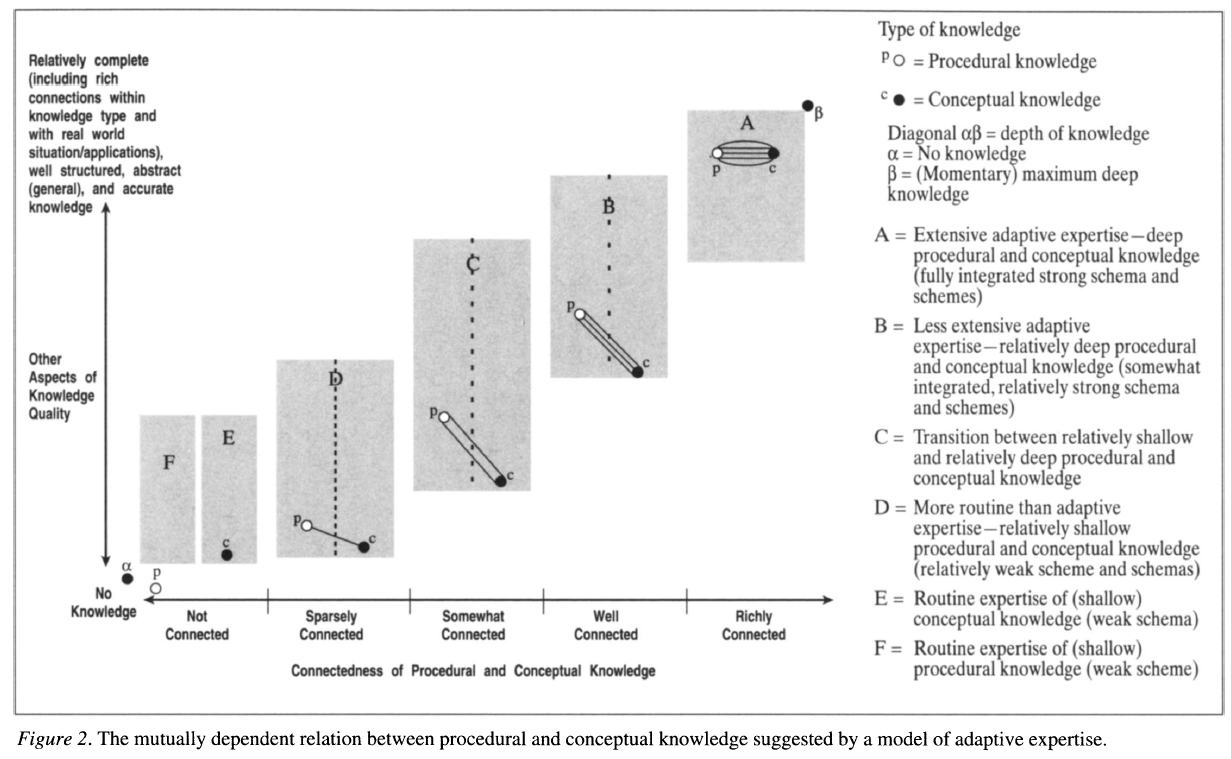
깊은 절차적 지식과 깊은 개념적 지식의 상호의존성
Interdependence of Deep Procedural and Deep Conceptual Knowledge
우리의 관점과 Star(2005) 또는 de Jong과 Ferguson-Hessler(1996)의 제안 간의 주요 차이점(그림 1의 B3 및 B4 셀에서 나타난 바)은, (상대적으로) 표면적인 절차적 및 개념적 지식은 (상대적으로) 독립적으로 존재할 수 있지만, (상대적으로) 깊은 절차적 지식은 (상대적으로) 깊은 개념적 지식 없이는 존재할 수 없다는 것입니다(Baroody, 2003). 개념적 지식과 절차적 지식 사이의 연결성 또는 상호 의존성의 정도는 그림 2의 수평축에 의해 나타납니다.
깊은 절차적 지식과 깊은 개념적 지식의 질
Quality of Deep Procedural and Deep Conceptual Knowledge
Star(2005)는 깊은 지식을 풍부하게 연결된 지식과만 동일시하는 경향이 있지만, de Jong과 Ferguson-Hessler(1996)는 지식의 질이 구조 수준(조직화의 정도), 추상성(적용의 일반성 또는 범위), 정확성 등도 포함할 수 있다고 제안합니다. 그림 2의 수직축은 지식의 질과 지식 완전성의 다른 측면들, 즉 지식 유형 내에서 또는 일상적 상황 및 적용과의 연결을 나타냅니다.
우리의 관점에서 이해의 깊이는 절차적 지식과 개념적 지식이 얼마나 상호 연결되어 있는지와 그 지식이 다른 측면에서 얼마나 완전하고, 잘 조직화되고, 추상적이며, 정확한지에 달려 있습니다. 그림 2에서 점 O(지식이 없음)에서 점 P(최대 지식)까지의 대각선은 이해의 깊이를 나타냅니다. 셀 F는 표면적인 절차적 지식(고립된 약한 체계)을 나타내며, 셀 E는 표면적인 개념적 지식(고립된 약한 체계)으로, 이해되지 않은 개념을 의미합니다. 셀 A는 깊은 지식을 나타내며(통합된 강한 체계), 셀 D, C, B는 절차적 지식과 개념적 지식이 서로 및 다른 지식의 측면과 점점 더 통합되는 과정을 나타냅니다(적응적 전문성 증가). 이와 함께 점점 더 잘 조직되고, 추상적이며, 정확한 지식의 네트워크가 형성됩니다.
큰 아이디어(Big Ideas)와 개념 및 절차의 이해
Big Ideas and Understanding Concepts and Procedures
큰 아이디어는 여러 개념, 절차, 문제를 연결하는 포괄적인 개념으로, 동일한 영역 내에서 또는 서로 다른 주제나 영역 간에 작용합니다(Baroody, Cibulsksis, Lai, & Li, 2004). 이러한 큰 아이디어는 개념과 절차를 깊이 이해하는 데 필수적이며, 다양한 기능을 수행합니다.
1. 여러 개념을 이해할 수 있는 기초 제공
큰 아이디어는 다양한 개념을 이해하는 기초를 제공합니다. 예를 들어, 균등 분할(equal partitioning)의 큰 아이디어 또는 비공식적 유사 개념인 공평한 분배(fair sharing)는 다음과 같은 개념을 이해하는 데 핵심적입니다:
- 단위 원리(Unit Principle): 무리수와 달리, 모든 자연수는 단위의 합으로 표현될 수 있으며(예: 5 = 1 + 1 + 1 + 1 + 1), 모든 유리수는 단위 분수의 합으로 표현될 수 있습니다(예: 3/5 = 1/5 + 1/5 + 1/5).
- 짝수(Even Number): 짝수 개의 항목은 정확히 두 사람이 공평하게 나눌 수 있습니다.
- 나눗셈(Division): 예를 들어, 특정 수의 사람들이 공평하게 나누었을 때 각 사람의 몫은 얼마인가?
- 분수(Fraction): 예를 들어, 3/4는 다음과 같이 볼 수 있습니다: 세 개의 사탕을 네 명의 사람에게 나눌 때, 각 사람의 몫은 얼마인가?
- 측정(Measurement): 길이나 면적과 같은 연속적인 양은 동등한 크기의 부분(단위)으로 나누어지고, 그 후에 이를 셀 수 있습니다.
- 평균(Mean): 모든 몫(점수)을 합친 후, 그 총량을 공평하게 나누어 각 사람(점수)의 몫이 무엇인지 찾습니다.
2. 다양한 절차에 대한 합리적 근거 제공
큰 아이디어는 아이들이 표준 알고리즘을 재발명하거나 자신만의 효율적인 절차를 발명하는 데 도움을 줄 수 있습니다. 예를 들어, 나눗셈을 공평한 분배라는 개념으로 이해함으로써 아이들은 긴 나눗셈 알고리즘을 재발명하거나 다자리 나눗셈 문제를 해결하기 위한 다른 효율적인 절차를 발명할 수 있습니다(예: Ambrose et al., 2003). 이러한 적응적 전문성(adaptive expertise)은 일상적인 상황에서 창의적인 전이를 제공할 수 있으며, 더 고급 개념이나 절차를 이해하거나 발견하거나 발명하는 데 기초를 제공합니다(Ambrose et al.; Baroody, 2003).
3. 여러 개념 및 절차를 연결하고 지식을 구조화하거나 재구조화할 수 있는 기초 제공
앞서 논의된 균등 분할의 예는 수 이론, 자연수 연산, 측정, 통계 등과 같은 주제를 연결합니다. 큰 아이디어는 아이들이 지식을 일관된 구조로 이해하도록 하며, 이를 고립된 개별 항목들의 연속으로 보는 대신 더 넓은 구조적 맥락에서 볼 수 있게 만듭니다. 특히, 학생들이 다양한 절차와 개념의 기저에 있는 구조를 바라보도록 장려합니다. 요약하자면, 큰 아이디어는 잘 조직되고, 추상적이며, 정확한 지식(즉, 개념적 및 절차적 지식)을 형성하는 데 필수적입니다.
연구에 대한 시사점
IMPLICATIONS FOR RESEARCH
Star(2005)의 관점(그림 1) 또는 우리의 대안적 재개념화(그림 2) 중 어느 것이 더 정확한지는 실증적으로 검증해야 할 문제입니다. Star의 관점에서 논리적 시사점은 절차적 유연성이 개념적 지식과 독립적으로 발달할 수 있다는 것입니다. 이는 절차의 단계에 대한 근거를 이해하지 못하더라도 상당한 전략 선택 또는 전이 지식이 가능함을 입증해야 합니다.
우리의 대안적 제안에서 논리적 시사점은, (상대적으로) 깊은 절차적 지식을 위해서는 적어도 어느 정도의 개념적 지식이 필요하며, 그 반대도 성립한다는 것입니다. 이에 따른 결과는 Baroody(2003)의 추측을 수정하는 것입니다: 개념적 지식과의 통합이 증가할수록 전략 선택과 적응력의 정확성, 다양성, 지속성, 일반성이 증가한다는 것입니다. 즉, 비개념적 지식과 주로 연결된 절차적 지식(그림 1의 B3와 B4 셀)은 개념적으로 연결된 절차적 지식보다 오류가 많고, 경직되며, 단기적이거나 고립된 결론을 도출할 가능성이 큽니다(Baroody, 2003; Carpenter, 1986).
두 번째 시사점은 지식의 유형 내에서 또는 유형 간의 연결을 구축하는 것만으로는 깊은 이해를 최대화하기에 충분하지 않을 수 있다는 것입니다. 문제를 구조화하거나 표상할 수 있는 지식의 질(구조화의 정도)을 고려해야 합니다(Davis, 1983; Gray, 1994; Greeno, Riley, & Gelman, 1984; Haapasalo, 2003; Rittle-Johnson, Siegler, & Alibali, 2001). 예를 들어, Peled와 Segalis(2005)는 절차적 유사성을 추상화하고 도메인 간 유사성을 매핑하는 것이 절차적 유사성만을 추상화하는 것보다 더 효과적이라는 것을 발견했습니다. 최근 대수학 연구에서는 산술 절차를 학습할 때 어떤 연결이 대수학 학습의 기초를 제공하며, 산술 절차를 유연하게 일반화하고 사용하는 데 중요한지를 탐구하고 있습니다(Carpenter et al., 1999; Romberg et al., 1999). 주요 발견은 명시적으로 인식되고 정당화될 수 있는 연결이 그렇지 않은 연결보다 더 강력하다는 것입니다(T. Carpenter, 개인적 의사소통, 2006년 8월 24일). 이와 관련된 시사점은 모든 연결이나 관계가 동일하지 않다는 것입니다. 일부는 이해 없이 형성될 수 있지만, 다른 일부는 어느 정도의 이해, 또 다른 일부는 상당한 이해가 필요합니다(Hiebert & Lefevre, 1986).
세 번째 시사점은 큰 아이디어(Big Ideas)가 연결의 본질, 구조, 또는 질을 이해하는 데 중요한 요소라는 것입니다. 이론적으로, 큰 아이디어는 많은 이해를 수반하는 연결을 제공해야 하며, 이는 도메인 내외의 절차와 개념을 연결하는 강력하고 일반적인 기초가 됩니다. 따라서 적응적 전문성을 촉진하는 데 중요한 역할을 합니다(Baroody et al., 2004). 실제로, 큰 아이디어에 기반한 교육은 전형적인 절차적, 개념적 또는 절차-개념 통합 교육보다 새로운 영역에서 자기 주도적이고 의미 있는 개념 및 절차 학습의 연쇄를 촉진할 수 있습니다. 예를 들어, 대수학을 산술 패턴과 관계를 일반화하고 표상하는 단축어로 이해하는 큰 아이디어에 초점을 맞춘 전문성 개발 프로그램은, 참여한 교사들이 학생들이 더 넓은 범위의 의미 있는 전략을 생성하고, 등호 기호와 같은 기호를 더 잘 이해하도록 도울 수 있음을 보여주었습니다(Carpenter & Franke, 2001; Jacobs, Franke, Carpenter, Levi, & Battey, 출간 예정).
결론적으로, de Jong과 Ferguson-Hessler(1996) 및 Star(2005)가 제안한 지식 유형과 질을 분리하고 연결성의 정도와 무관하게 절차적 및 개념적 지식을 정의하자는 권고는 타당합니다. 그러나 수학적 절차와 개념에 대한 의미 있는 지식을 서로 밀접하게 연결된 필수적인 관계로 보는 것이 심리학적, 교육학적으로 더 합리적입니다. 개념적 이해는 절차적 유창성을 포함한 수학적 능숙성의 모든 측면에 중요한 기초라는 주장이 가능합니다(Baroody, 2003). 또한 큰 아이디어는 수학적 능숙성의 모든 측면을 촉진하는 데 특히 중요합니다. 심리학자들은 오래전부터 의미 있는 암기가 기계적인 암기보다 사실 및 절차적 지식의 유지와 전이를 더 효과적으로 보장하는 방법이라는 것을 알고 있었습니다(Ginsburg, 1977; Katona, 1967; Skemp, 1978; Wertheimer, 1959). 절차적 지식을 개념적 지식과 연결하는 것은 학습을 더 쉽게 하고, 계산상의 지름길을 제공하며, 오류를 줄이고, 망각을 방지하는 데 도움이 될 수 있습니다(즉, 효율성을 촉진합니다). 절차를 이해하는 아이들은 실제 응용 사례를 더 잘 인식하고, 기존 지식을 새로운 도전이나 문제에 맞추어 조정할 가능성이 더 높습니다. 이는, 부분적으로, National Research Council(Kilpatrick et al., 2001)이 수학적 능숙성의 요소를 상호 연결된 방식으로 가르칠 것을 권장한 이유입니다.
'Wilson Centre' 카테고리의 다른 글
| [QI] 현명한 단어 선택: 불필요한 시험에 대한 대화에서 전공의들이 수사학적 호소를 사용하는 이유 (1) | 2024.09.12 |
|---|---|
| [QI] 21세기를 위한 아동 건강 개선과 품질 개선의 조화 (0) | 2024.09.12 |
| [Expertise] 전문성과 지식의 인지적 은유: 의학교육의 전망과 한계 (0) | 2024.09.12 |
| [양적연구] 연구를 위한 실험 및 준실험 설계 (0) | 2024.09.12 |
| [양적연구] 의학교육의 정량적 연구 방법 (2) | 2024.09.12 |
